
If you must have a high Rin, then consider a Darlington. Pick a very large Ce, to ensure Zc << 2.6 ohms.įor high bandwidth, you might worry about C_Miller_Effect.Īt high frequencies, that charge consumption will suck up lots of input energy. With 130 ohms as Rcollector, we will mostly ignore the Rload value in computing the Voltage Gain. For a gain of 50, set Rc = 50 * 2.6 ohms, or 130 ohms. You have no required Vout_peakPeak, despite that Rload.īias the transistor to 10mA (why not? power is free).

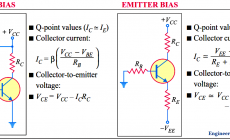
Fixed bias is also known as base resistor bias. Since 12/0.026 is about 480, then yes, we can move ahead.īias the transistor emitter to VDD/3. Fixed bias circuit Collector to base bias Potential divider bias. The maximum gain a single bipolar can provide, with resistive load, is Hang in there.įor a gain of 50X, using a single transistor, with resistive load, first let us be sure we can achieve that 50X. Transistor Amplifier with Impedance Matching Transformer, David E. Your instructor is letting you immerse, and learn quickly. If you have NO emitter bypassing, then Rin is beta * (1/gm + Re). The transistor Rin, assuming excellent bypassing of Re, will be Beta/gm where gm is the transistor transconductance. Input Resistance will be parallel combination of R1, R2, and the transistor Rin. These 2 Rs allow stabile biasing and stable Gain.Īnd thanks to LvW for error detection and system thinking.
#Ce transistor biasing with emitter feedback circuit series
[For best design, add a 2nd Re in series with first R, with no bypassing. In practice I suspect that designers tend to take more of a heuristic approach to circuit design rather than solve equations like this. I find that my courses at university are very theoretical and so I tend to over complicate the designs.

I'd also be interested to know how more experienced designers would approach this simple design problem. Could anyone explain what is happening here? I would expect these values to be the same as what I worked them out to be previously from the voltage gain equation ( \$92 \Omega \$)? In simulation this method seems to work however I can't understand how the input and thevenin resistances have seemingly changed value. I calculate \$ \beta = \frac = 5357 \Omega\$ I want to keep that low so I choose \$2mA\$ and plot the IC vs VCE curves for this specific transistor in a spice simulator:Ĭhoosing a point half way on the load line for symmetrical swing, I obtain: I began my design by picking a maximum current. For an emitter feedback bias Circuit having, RE1Kohm, RC 4.7Kohm, IB0.005mA, IE 1mA, VCC 12V and Vce 5V. I've drawn the small-signal model as follows, assuming that in the midband coupling capacitors are treated as shorts and bypass and load capacitors are treated as open circuits: Using a 2N2222 BJT transistor and the following CE configuration: 1.For emitter bias, the voltage across the emitter resistor is the same as the voltage between the emitter and the 2. Load \$5k\Omega\$ with a coupling capacitor (not shown below).I am trying to design a Common-Emitter amplifier to the following specifications:


 0 kommentar(er)
0 kommentar(er)
